Untuk mendapatkan gradien dari suatu garis lurus, kita harus melakukan beberapa langkah agar tercapai rumus umum persamaan garis lurus.
Konsep yang dipakai
Untuk bisa menentukan gradien suatu garis lurus, maka persamaan garisnya haruslah memenuhi rumus umum berikut.
y = mx + c
Perhatikan :
- Di ruas kiri, di sebelah kiri tanda sama dengan, hanya ada variabel "y" saja. Tidak boleh ada temannya.
- Dan angka di depan "y" haruslah 1.
Ingat bahwa 1y = y - Di ruas kanan, di sebelah kanan tanda sama dengan, suku selain "y" ditempatkan di sini.
Ketika sudah berbentuk rumus umum di atas, maka gradiennya adalah "m".
"m" adalah angka di depan variabel x.
Atau "m" adalah koefisien dari variabel "x".
Contoh soal
Agar semakin mengerti, kita coba contoh soalnya.
Soal :
1. Carilah gradien garis dari persamaan garis lurus : 2y - 4x = 6!
1. Carilah gradien garis dari persamaan garis lurus : 2y - 4x = 6!
Baik, mari kita kerjakan!!
2y - 4x = 6
- Yang boleh di ruas kiri hanyalah variabel "y"
- Selain "y" harus dipindah ke ruas kanan
- Jadi, - 4x harus dipindah ke ruas kanan
Ketika - 4x dipindah ke ruas kanan, maka tandanya berubah dari minus menjadi plus. Sehingga -4x berubah menjadi +4x
Tips!Setiap pindah ruas, maka tanda berubah
2y = 4x + 6
- 6 tidak pindah, jadi tandanya tetap seperti sebelumnya, yaitu positif (+)
- Di ruas kiri, variabel "y" masih memiliki angka 2. Ini belum memenuhi rumus umum. Jadi, semua suku harus dibagi dengan 2.
Mengapa dibagi 2?
Karena sesuai dengan angka yang melekat pada "y". Agar angka di depan "y" diperoleh 1.
2y÷2 = 4x÷2 + 6÷2
- Setiap suku dibagi 2
- 2y dibagi 2
- 4x dibagi 2
- 6 dibagi 2
y = 2x + 3
Nah...
Bentuk terakhir ini sudah sesuai dengan rumus umum gradien.
Kita tinggal menentukan gradiennya yang mana.
Ingat!!
Gradien adalah angka di depan "x" atau koefisien dari "x".
Gradien (m) = 2.
Bagaimana, mudah bukan??
Soal :
2. Tentukan gradien dari persamaan garis berikut : 8x - 4y = 12!
2. Tentukan gradien dari persamaan garis berikut : 8x - 4y = 12!
Langkahnya masih sama seperti soal pertama.
Tulis dulu persamaan garisnya.
8x - 4y = 12
- Selain suku yang mengandung "y", harus dipindah ke ruas kanan
- Berarti kita pindahkan 8x
- 8x dipindah ke ruas kanan menjadi -8x, karena tanda sebelumnya positif dan jika dipindah akan berubah menjadi negatif
- Sedangkan 12 tidak dipindah karena sudah ada di ruas kanan
-4y = -8x + 12
- Tanda minus (-) dari -4y diperoleh dari tanda kurang yang ada di depannya. Karena tidak ikut berpindah, maka tanda minusnya tetap.
Selanjutnya :
- Di depan "y" masih ada bilangan -4 yang melekat.
- Sehingga semua suku harus dibagi dengan -4, sesuai angka di depan variabel "y".
- -4 ÷ -4 = 1 (minus bagi minus adalah positif)
- -8 ÷ -4 = 2 (minus bagi minus adalah positif)
- 12 ÷ -4 = -3 (positif bagi minus adalah negatif)
Bentuk akhir yang sesuai dengan rumus umum adalah :
y = 2x - 3
Di depan y sudah tidak terlihat angka lagi, sebenarnya angka di depan "y" adalah 1. Tapi boleh tidak ditulis.
Dan kitapun bisa dengan mudah menentukan gradiennya, yaitu angka di depan variabel x.
Gradien (m) = 2.
Jadi, itulah cara mencari gradien jika diketahui persamaan garisnya.


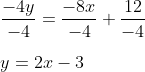
Posting Komentar untuk "Mencari gradien dari persamaan garis : 2y - 4x = 6"